Magnitude of Stars

Apparent Magnitude

Early Greek astronomers used a scale of magnitude devised by Hipparchus around the 2nd century BC, which was based on how bright stars appeared with the naked eye. The Hipparchus scale went from magnitude 1, for the brightest stars, up to magnitude 6, for those stars which were barely visible.

When telescopes were invented, it was possible to compare the intensities of the light from stars and it was found that the brightest stars of magnitude 1, were around 100 times the intensity of the faintest stars at magnitude 6. Therefore, each magnitude was, 100 = x5. Then each increase in magnitude was 2.512 times fainter than the last. Telescopes allowed astronomers to observe much fainter stars and now the apparent magnitude scale goes from s to around f,

The apparent brightness of a star is how bright it seems when viewed from the Earth, but a large bright star can appear dim if it is a long way from the Earth and a dim star can appear to be bright if it is close to the Earth, therefore the apparent magnitude has no bearing on the distance from the Earth.

To give an acurate measurement of the brightness of a star we need to make an absolute magnitude scale. The absolute magnitude is how bright a star is when viewed from a distance of 10 parsecs.

In order to find the absolute magnitude we need to know the distance of the star from the sun, how do we do this? The intensity of light decreases with distance from the star. The rate at which it decreases is inversely proportional to the square of the distance. Thus if we have a star of luminosity L if we move a distance d the same quantity of light has to cover a larger spherical area. Therefore, away the intensity I = L/(4πd2).

(1)

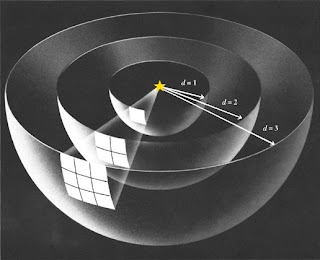The inverse square law for the intensity of light

The apparent magnitude m is given by

(2)

m = - 2.5 log10(I + c)(2)

Where, I is the observed intensity of the object.

From the properties of logarithms, the ratio of the intensities of two stars is.

m1 - m2 = - 2.5 [log2.5(I1) - log10(I2)]

(3)

m1 - m2 = - 2.5 log2.5(I1/I2)(3)

Absolute Magnitude

"The absolute magnitude is the brightness of a star at a distance of 10 parsecs".

M = m - 2.5 log10(I2/102)

(4)

M = m - 5 log(I/10)(4)
Absolute Magnitude and Distance

The relationship between the apparent magnitude and the absolute magnitude is given by

M = m - 5 log10(d/10)

From this equation we can calculate the distance d from the Earth if we know the absolute magnitude. In practise we don't know the absolute magnitude because we cannot travel 10 parsecs from the star in question. We can use several indirect methods to determine its absolute magnitude. If the star is on the main sequence of stars then we can determine the brightness from its parallax.